Mathe-AG
DIE MATHE-AG im Schuljahr 2025/
Zuvor findet am Freitag, dem 17.10 unser Tag der Mathematik statt.
Mathe-AG Termin:
Freitag, 15:30 – 17:00 Uhr. (außer Schulferien in BW)
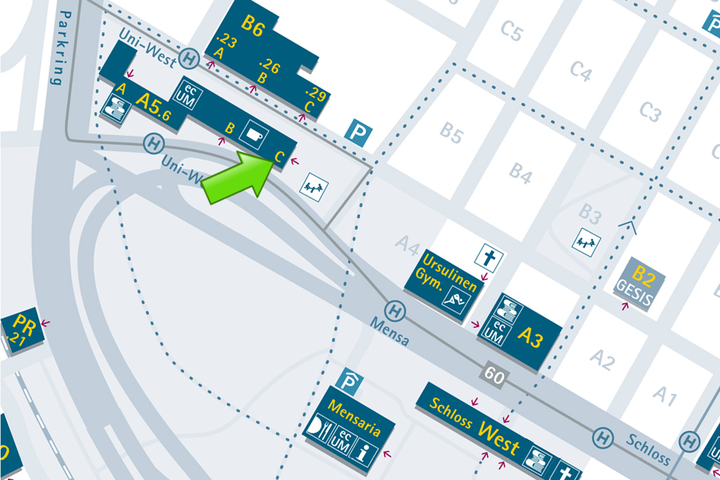
Die Mathe-AG findet statt in:
Universität Mannheim, A 5, 6 Bauteil C, Raum C 012 (Glasgebäude, Raum von außen einsehbar, wegen Baustelle Eingang auf der anderen Seite vom Gebäude, Eingang neben dem Café Soleil !)
Für Interessierte ab der Klassenstufe 9 (oder jünger!).
Bei Interesse einfach vorbeikommen oder schreiben Sie an Peter Parczewski
In den ersten Wochen erkunden wir die Themen der Aufgaben von unserem Tag der Mathematik 2025. Weitere Themen werden sein:
- Grundbegriffe Aussagen, Mengen und Funktionen
- Grundbegriffe Kombinatorik
- Beweise und Beweismethoden
- Grundbegriffe Analysis
- …
Mathe-AG Schuljahr 2025/
Programm
Die genauen Themen ergeben sich dynamisch und in Absprache mit den Teilnehmenden.
Die geplanten Themen im Schuljahr sind:
- Probleme und Verallgemeinerungen der Aufgaben vom Tag der Mathematik 2025
- Mathematische Grundbegriffe (Aussagen, Mengen, Funktionen)
- Abzählen und Kombinatorik, kombinatorische Beweise, Permutationen, Mengen-Partitionen, Stirling-Zahlen
- Analysis (Folgen, Reihen, Konvergenz, Stetigkeit)
- Lineare Algebra (Gruppen, Homomorphismen, Vektorräume)
- Exkurse (mathematische Logik, metrische Räume, topologische Räume)
- Exkurse Analysis (Komplexe Zahlen, Differenzierbarkeit, Integrierbarkeit)
- Exkurse Stochastik und Numerik (Interpolation, numerische Integration, Monte Carlo Methoden)
DIE MATHE-AG im Schuljahr 2025/
2026 endet voraussichtlich Juni mit einem mathematischen Workshop oder mit dem Tag der Mathematik 2026. Termine und Inhalte
Termine der Mathe-AG
- Treffen am 24.10.25
- Treffen am 31.10.25 entfällt (Ferien in BW)
- Treffen am 07.11.25
- Treffen am 14.11.25
- Treffen am 21.11.25
- Treffen am 28.11.25
- Treffen am 05.12.25
- …
Uni Mathe-AG Schuljahre 2017 – 2025
Themen
Die Themen waren u. a.:
- Probleme mit Kacheln und Fliesen
- Fibonacci-Zahlen, kombinatorische Beweise, allgemeine Rekursionen
- Grundbegriffe Mathematik (Aussagenlogik, Mengen, Funktionen, Beweismethoden)
- Teppichsatz und Beweise mit Figuren
- Summenformeln und Bildbeweise
- Axiome und Beweismethoden
- Bildbeweise
- Musterbildung in der Biologie : Reaktions-Diffusions-Modelle
- Schachbrettprobleme und Färbungsprobleme
- Probleme über Flächen von Mondsicheln/
Pythagoras für Halbkreise und andere Figuren - Probleme über Ellipsen und Monde/
Exkurs Höhensatz Beweise - Satz von Pick und Quadrate im Dreieck
- Umfang Ellipse : Sätze zum Pizzatheorem
- Kleinsche Flasche und Topologie
- Sheldon Vermutung, Sheldon Primzahl 73 (Sheldon Coopers beste Zahl)
- Weyl Gleichverteilung modulo 1
- Mersenne Primzahlen und der kleine Satz von Fermat
- Entfernungen, Metriken und die Dreiecksungleichung
- Spiele und Strategien
- Zufall, Stochastik und Monte Carlo Methoden
- Binomialsatz und Kombinatorik
- Sind fast alle Dreiecke stumpfwinklig?
- Schubfachprinzip
- Mathematische Logik: Prädikatenlogik
- Mathematische Logik: Vollständigkeitssatz
- Mathematische Logik: Mengen, Unendlichkeiten, Cantor und Hilberts Hotel
- Analysis: Grundlagen, Aussagenlogik, Mengen
- Analysis: Funktionen, Beweismethoden
- Analysis: Axiome der reellen Zahlen, komplexe Zahlen
- Analysis: Folgen Konvergenz und Limesregeln
- Analysis: Folgen Limes-Ungleichung und wichtige Grenzwerte
- Analysis: Folgen Existenzsätze
- Analysis: Folgen Aufgaben
- Analysis: Reihen und Konvergenzkriterien
- Analysis: Gamma-Funktion und Zeta-Funktion